반응형
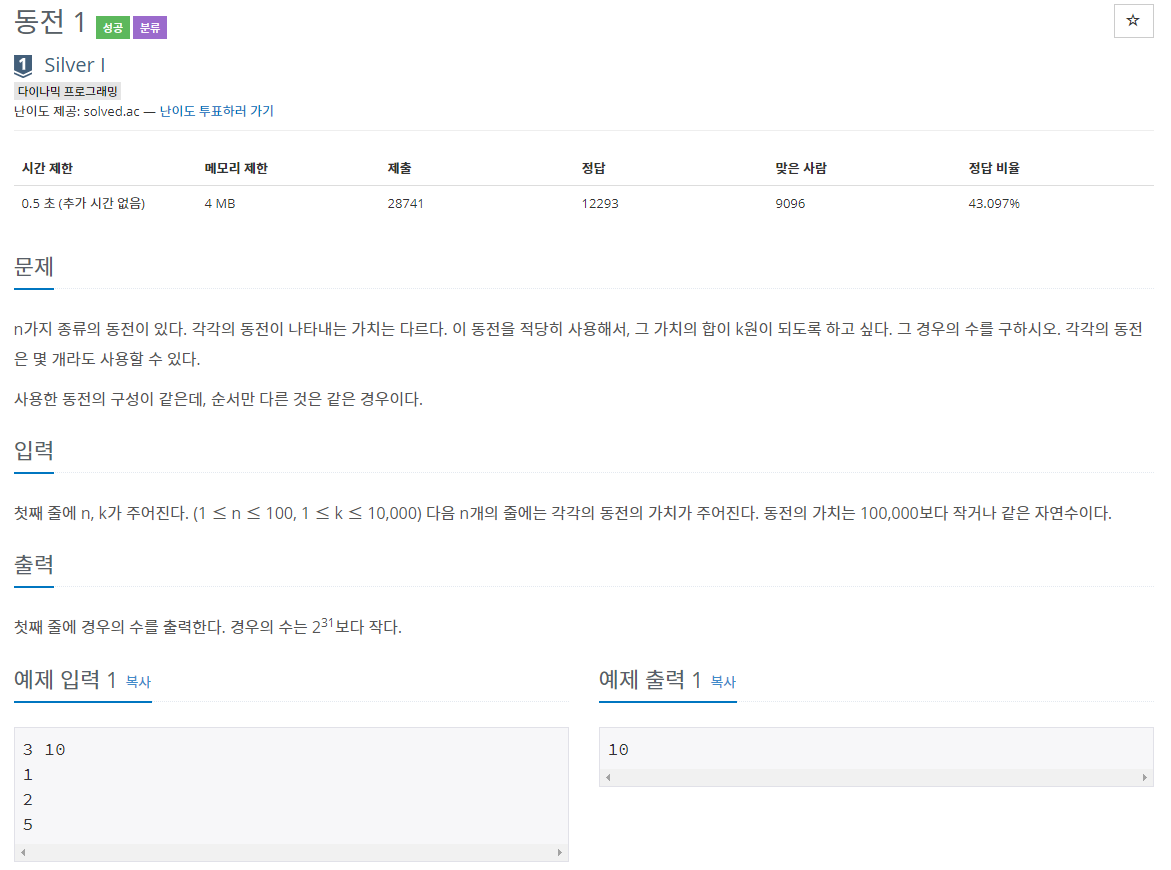
다이나믹 프로그래밍 문제이다.
1차원 DP문제로써 점화식을 세우는데 오래걸리진 않았다. 각 k 에선 k-동전가치 만큼에서 경우들을 더해주면 구할 수 있으므로 다음과 같은 점화식을 구했다.
for 1부터 k까지
for 모든 동전가치
dp[k] = dp[k] + dp[k-동전가치]
하지만 이문제에선 하나의 조건이 더 있는데 바로 동전의 구성이 같다면 카운팅을 안해주는 것이었다. 바로 중복의 경우르를 제거해주는 것인데, 이것을 어떻게 구현할지 한참을 고민하였다. 답은 바로 1부터 k까지가 아니라 모든 동전에 대해서 먼저 처리를 해주는 것이었다.
for 모든 동전가치
for 1부터 k까지
dp[k] = dp[k] + dp[k-동전가치]
다음과 같은 점화식으로 풀 수 있는 문제였다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
package study4;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main_bj_2293_동전1 {
static int N;
static int K;
static long[] dp;
static int[] coins;
public static void main(String[] args) throws Exception {
BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st= new StringTokenizer(br.readLine());
N=Integer.parseInt(st.nextToken());
K=Integer.parseInt(st.nextToken());
coins=new int[N];
for(int i=0;i<N;i++) {
coins[i]=Integer.parseInt(br.readLine());
}
dp=new long[K+1];
dp[0]=1;
for(int j=0;j<N;j++ ) {
for(int i=1;i<=K;i++) {
if(i-coins[j]>=0) {
dp[i]=dp[i]+dp[i-coins[j]];
}
}
}
System.out.println(dp[K]);
}
}
|
반응형
'Algorithm' 카테고리의 다른 글
| [BOJ] 1786. 찾기 (0) | 2020.09.04 |
|---|---|
| [Programmers] 괄호 변환 (0) | 2020.09.03 |
| [Programmers] 경주로 건설 (0) | 2020.08.31 |
| [Programmers] 보석 쇼핑 (0) | 2020.08.31 |
| [Programmers] 수식 최대화 (0) | 2020.08.31 |