반응형
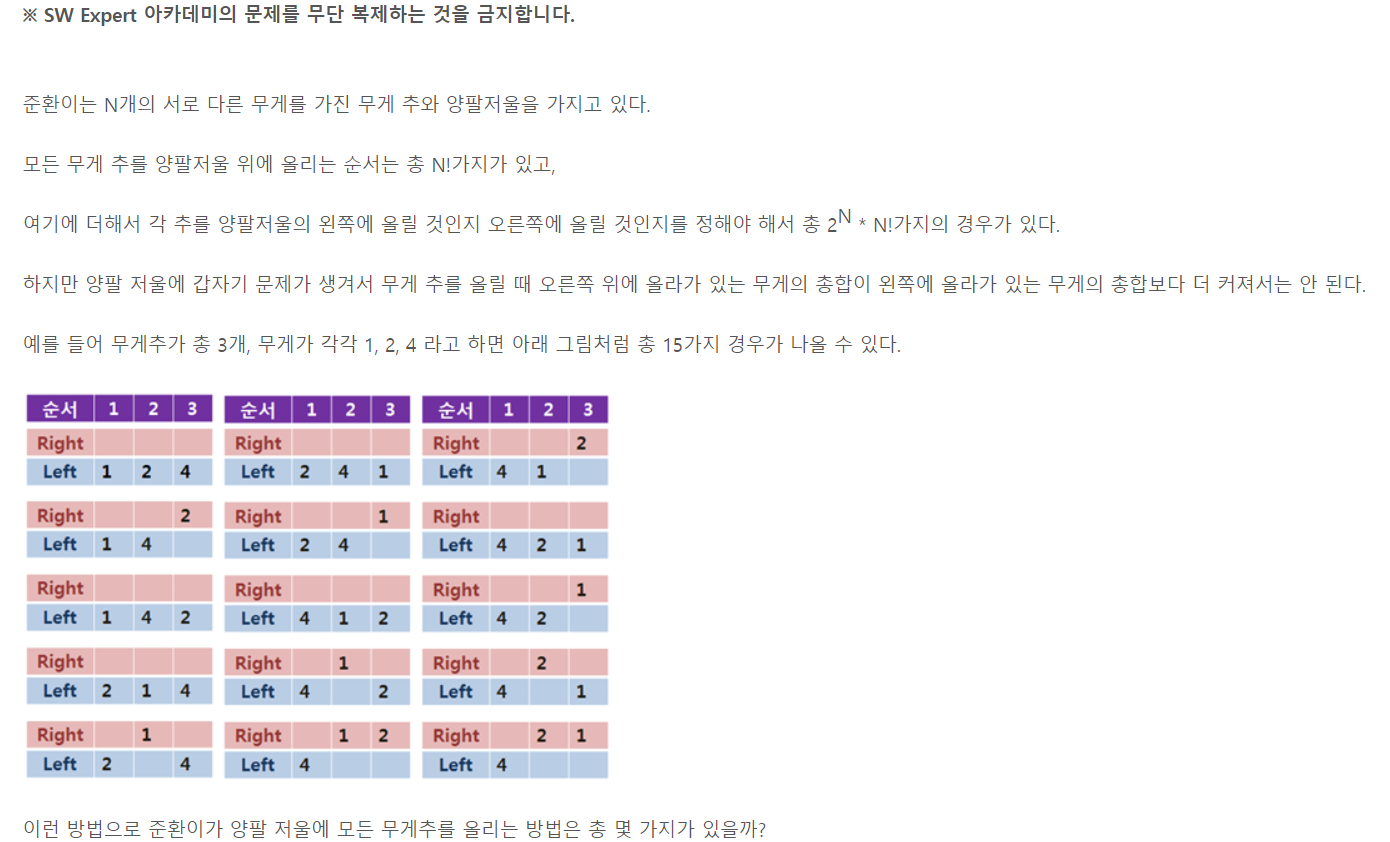

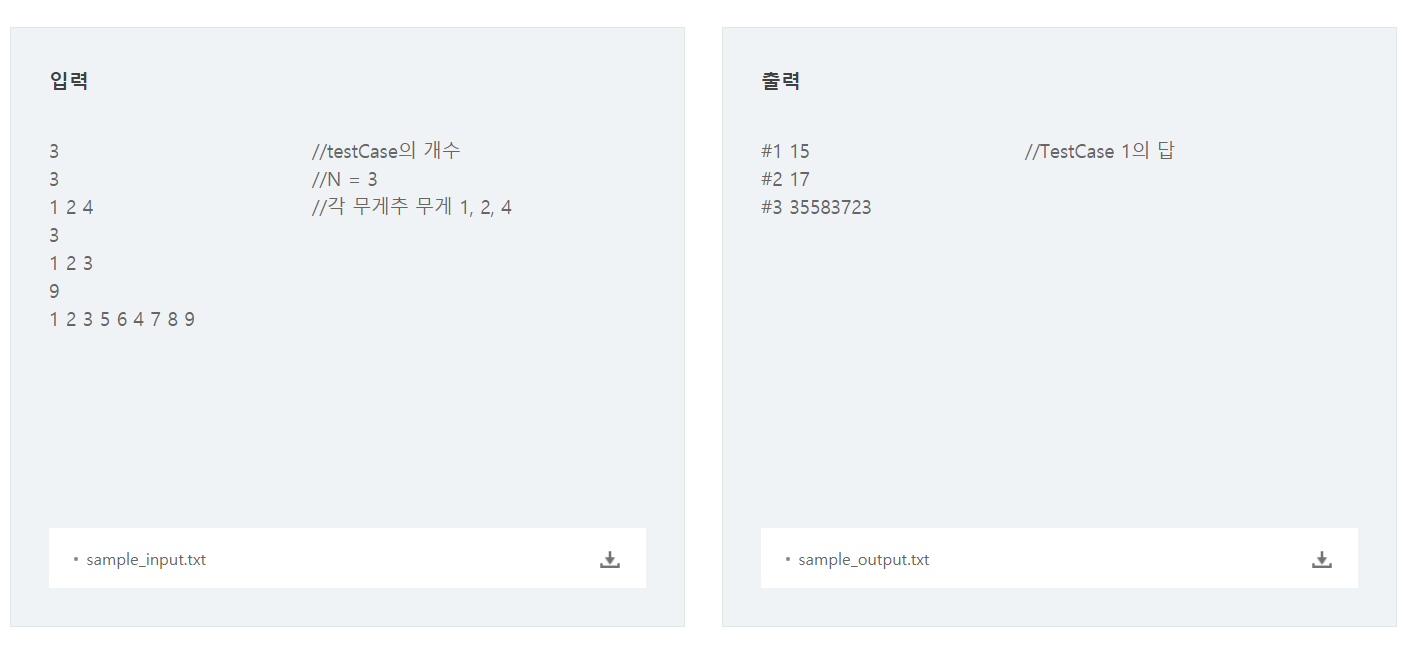
순열 재귀를 이용하여 푸는 문제이다.
주어진 추를 왼쪽에 놓을때, 오른쪽에 놓을때의 경우를 재귀로 호출하며 풀수있는 문제이다. 다만 여기서 주의할점이 있다. 저울이 양쪽이기에 N개의 추가 있다면 2^N * N!을 총가지수로 가지기 때문에 가지치기가 상당히 중요한 문제이다. 따라서 다음과 같은 가지치기를 하였다. 우선 오른쪽저울에 추가해도 왼쪽저울을 안넘을때 오른쪽 저울에 추가하는 가지치기와 만일 현재왼쪽의 총합*2가 sum을 넘는다면 뒤쪽은 다안보고 한번에 모든 경우를 더해주는 방식으로 가지치기를 하여 시간초과를 통과하였다.
단순한 재귀 문제이지만 가지치기를 하는 방식을 곰곰히 생각해봐야하는 문제이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
|
package swea;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Solution_d4_3234_준환이의양팔저울 {
static int[] numbers;
static boolean[] visit;
static int N;
static int count;
static int sum;
public static void main(String[] args) throws Exception {
BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
int T=Integer.parseInt(br.readLine());
for(int tc=1;tc<=T;tc++) {
N=Integer.parseInt(br.readLine());
numbers=new int[N];
visit=new boolean[N];
sum=0;
st=new StringTokenizer(br.readLine());
for(int i=0;i<N;i++) {
numbers[i]=Integer.parseInt(st.nextToken());
sum+=numbers[i];
}
count=0;
perm(0,0,0);
System.out.println("#"+tc+" "+count);
}
}
static void perm(int depth,int left, int right) {
if(depth==N) {
count+=1;
return;
}
if(sum - left <= left) {
count+=fact(N-depth) *Math.pow(2, N-depth);
return;
}
for(int i=0;i<N;i++) {
if(visit[i]==false) {
visit[i]=true;
perm(depth+1,left+numbers[i],right);
visit[i]=false;
if(left >= right+numbers[i]) {
visit[i]=true;
perm(depth+1,left,right+numbers[i]);
visit[i]=false;
}
}
}
}
static int fact(int num) {
int answer=1;
for(int i=num;i>=1;i--) {
answer*=i;
}
return answer;
}
}
|
반응형
'Algorithm' 카테고리의 다른 글
| [BOJ] 17069. 파이프 옮기기 2 (0) | 2020.05.30 |
|---|---|
| [SWEA] 5215. 햄버거 다이어트 (0) | 2020.05.29 |
| [BOJ] 17142. 연구소 3 (0) | 2020.05.29 |
| [BOJ] 1987. 알파벳 (0) | 2020.05.27 |
| [BOJ] 2580. 스도쿠 (0) | 2020.05.27 |