반응형

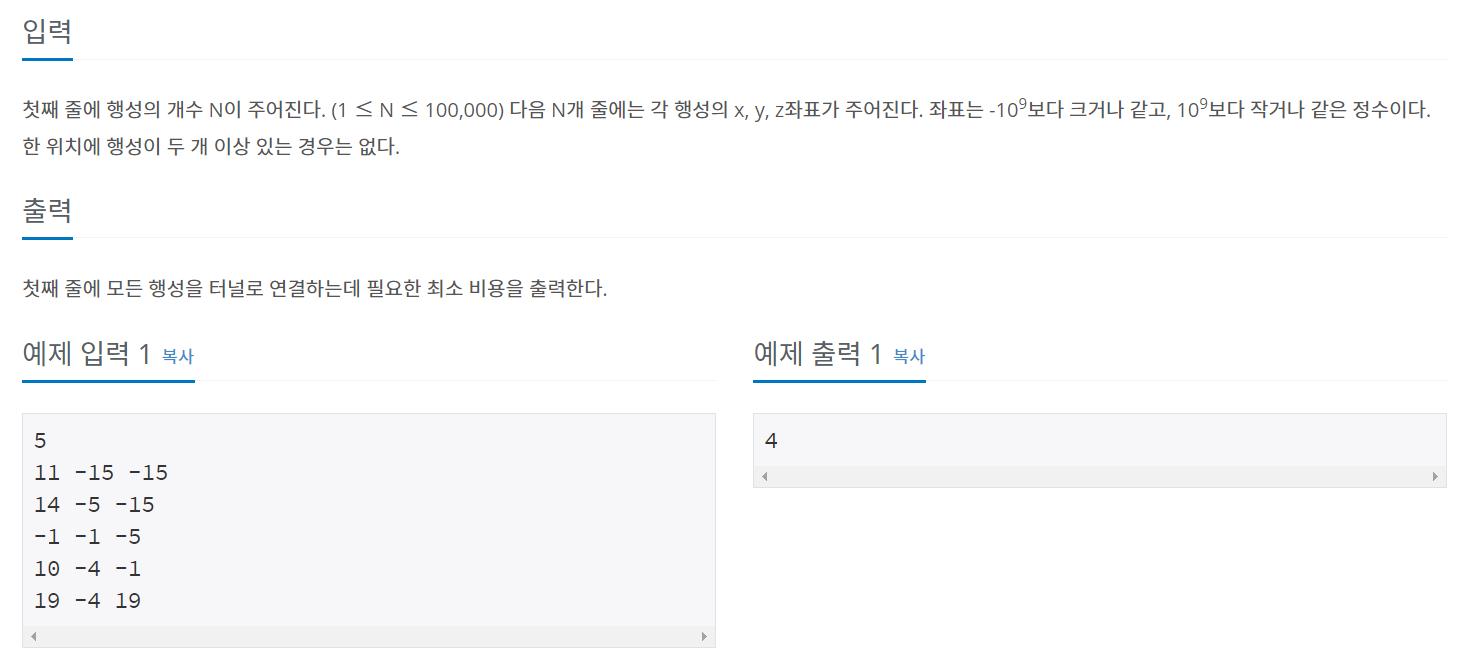
모든 정점을 N-1개로 연결하는 MST 문제이다.
MST를 해결하기 위해선 간선기준인 Kruskal 알고리즘과 정점기준인 Prim 알고리즘을 사용할 수 있다. 두 문제는 어쨋든 출발점, 도착점 비용을 알아야하기 때문에 문제에서 비용을 구하는 방법을 생각해보았다. N이 최대 100,000임으로 2중for문은 사용불가하여 고민해본 결과, 전체 정점을 x,y,z로 각 각 정렬했을때 하나 뒤의 정점과의 x,y,z 차이를 이용하여 간선을 구하는 방법을 고안하였다. 이렇게 모든 간선들의 비용을 PriorityQueue에 저장한다음 UnionFind를 이용하여 MST를 구하였다.
그래프의 간선들을 만듬에 있어 충분한 고민이 필요했던 문제였다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
|
package boj2;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main_bj_2887_행성터널 {
static int N;
static PriorityQueue<Edge> pq;
static Pos[] arr;
static int[] p;
static int count;
static int distance;
static class Pos{
int index,x,y,z;
Pos(int i,int x,int y,int z){
index=i;this.x=x;this.y=y;this.z=z;
}
}
static class Edge implements Comparable<Edge>{
int u,v,w;
Edge(int u,int v,int w) {
this.u=u;this.v=v;this.w=w;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(w, o.w);
}
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st =null;
N=Integer.parseInt(br.readLine());
arr=new Pos[N];
pq=new PriorityQueue<>();
for(int i=1;i<=N;i++) {
st=new StringTokenizer(br.readLine());
int x=Integer.parseInt(st.nextToken());
int y=Integer.parseInt(st.nextToken());
int z=Integer.parseInt(st.nextToken());
arr[i-1]=new Pos(i, x, y, z);
}
makeEdges();
p=new int[N+1];
count=0;
distance=0;
kruskal();
System.out.println(distance);
}
static void makeEdges() {
Pos start=null;
Arrays.sort(arr,new Comparator<Pos>() {
@Override
public int compare(Pos o1, Pos o2) {
return Integer.compare(o1.x,o2.x);
}
});
start=arr[0];
for(int i=1;i<N;i++) {
pq.add(new Edge(start.index, arr[i].index, Math.abs(start.x-arr[i].x)));
start=arr[i];
}
Arrays.sort(arr,new Comparator<Pos>() {
@Override
public int compare(Pos o1, Pos o2) {
return Integer.compare(o1.y,o2.y);
}
});
start=arr[0];
for(int i=1;i<N;i++) {
pq.add(new Edge(start.index, arr[i].index, Math.abs(start.y-arr[i].y)));
start=arr[i];
}
Arrays.sort(arr,new Comparator<Pos>() {
@Override
public int compare(Pos o1, Pos o2) {
return Integer.compare(o1.z,o2.z);
}
});
start=arr[0];
for(int i=1;i<N;i++) {
pq.add(new Edge(start.index, arr[i].index, Math.abs(start.z-arr[i].z)));
start=arr[i];
}
}
static void kruskal() {
for(int i=1;i<=N;i++)
p[i]=i;
while(!pq.isEmpty()) {
Edge edge=pq.poll();
if(find(edge.u)!=find(edge.v)) { //부모가 다르다면 픽
union(edge.u, edge.v);
count+=1;
distance+=edge.w;
}
if(count==N-1)
break;
}
}
static int find(int num) {
if(p[num]==num)
return num;
return p[num]=find(p[num]);
}
static void union(int num1,int num2) {
num1=find(num1);
num2=find(num2);
if(num1<num2)
p[num2]=num1;
else
p[num1]=num2;
}
}
|
반응형
'Algorithm' 카테고리의 다른 글
| [Programmers] 프렌즈4블록 (0) | 2020.05.21 |
|---|---|
| [Programmers] 셔틀버스 (0) | 2020.05.17 |
| [BOJ] 11660. 구간 합 구하기5 (0) | 2020.05.16 |
| [BOJ] 10775. 공항 (0) | 2020.05.15 |
| [BOJ] 1976. 여행 가자 (0) | 2020.05.15 |