반응형
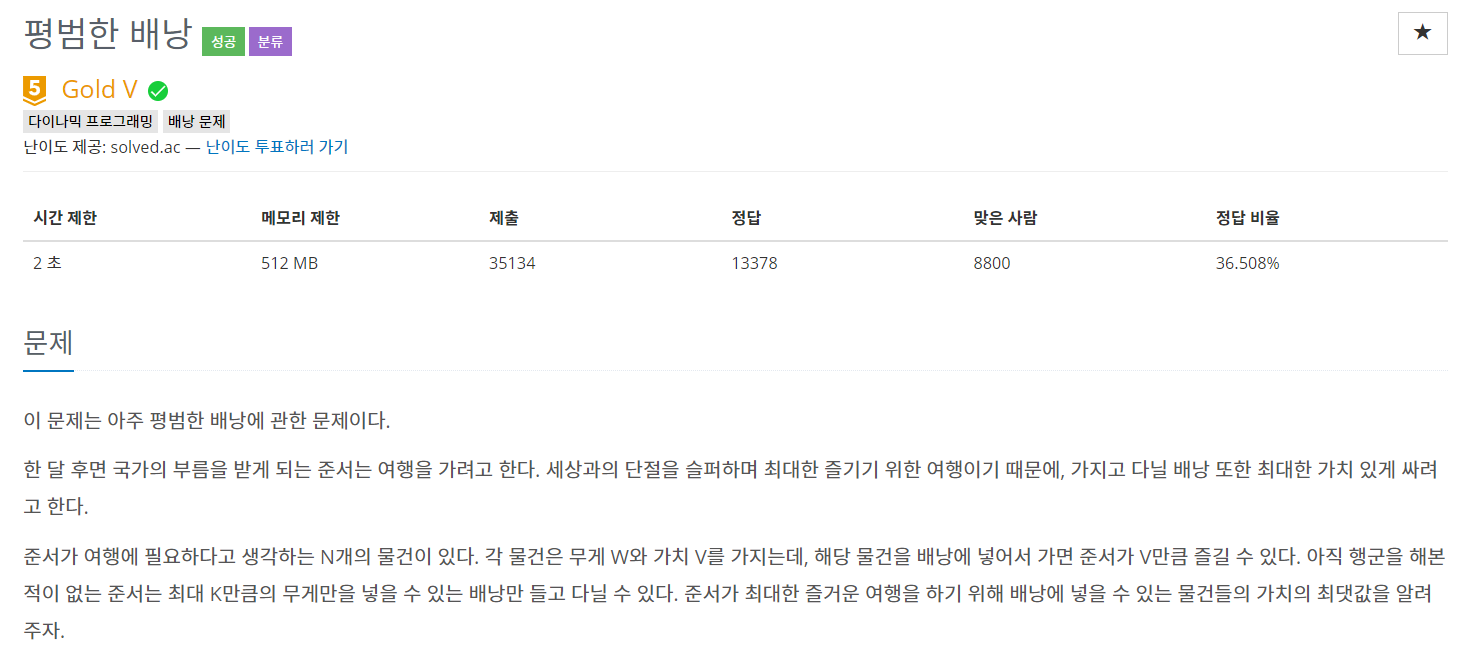
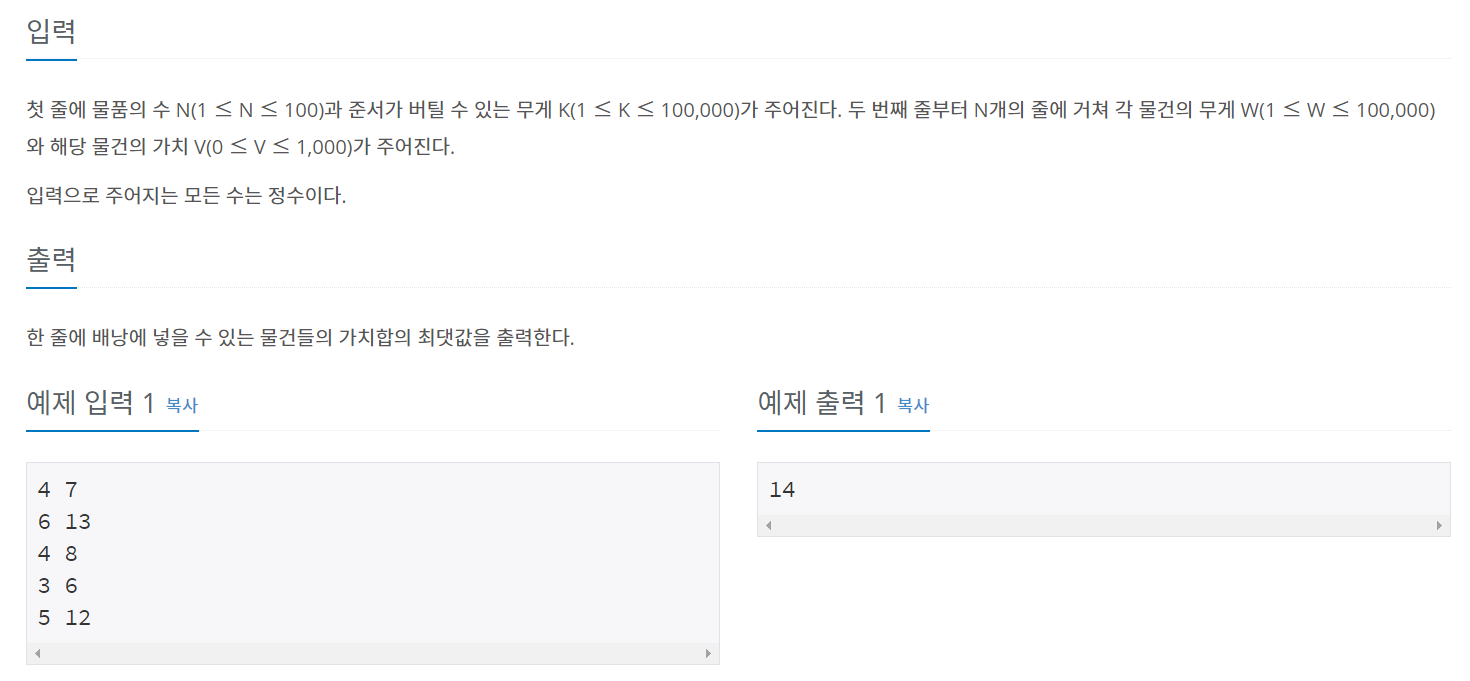
유명한 Knapsack 문제이다.
Knapsack 대표적인 문제이다. 보통 Knapsack 문제를 접근할때는 크게 두가지 방법이 있다. 크게 브루트포스와 dp로 접근할 수 있다.
브루투포스로 접근은 단순하게 고르고, 안고르고를 반복하며 재귀호출하는 방식이다. 이 방식은 시간복잡도가 2^N 이기에 대다수의 문제에서 적용이 힘들다. 이 문제또한 N의 최대값이 100이기에 적용이 불가하지만 한번 코드는 작성해보았다.
1. 브루트 포스(시간초과)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
package algostudy2;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main_bj_12865_평범한배낭_timeout {
static int N;
static int weightLimit;
static int[] weight;
static int[] value;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
weightLimit = Integer.parseInt(st.nextToken());
weight = new int[N];
value = new int[N];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
weight[i] = Integer.parseInt(st.nextToken());
value[i] = Integer.parseInt(st.nextToken());
}
System.out.println(dfs(0, 0));
}
static int dfs(int depth, int weightSum) {
if (depth == N) {
return 0;
}
int valueSum1 = 0;
if (weightSum + weight[depth] <= weightLimit) {
valueSum1 = value[depth] + dfs(depth + 1, weightSum + weight[depth]);
}
int valueSum2 = dfs(depth + 1, weightSum);
return Math.max(valueSum1, valueSum2);
}
}
|
다음 방식으로 이 재귀 과정에서 메모이제이션 dp를 활용하는 방식을 사용해보았다. 즉, dp[depth][weight]을 활용하여 만일 한번 탐색된 곳이면 저장 후 이것을 다시 탐색하지 않고 반환해주는 방식을 사용해보았다.
2. 재귀 + dp
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
package algostudy2;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main_bj_12865_평범한배낭_dp1 {
static int N;
static int weightLimit;
static int[] weight;
static int[] value;
static int[][] dp;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
weightLimit = Integer.parseInt(st.nextToken());
weight = new int[N];
value = new int[N];
dp = new int[101][100001]; //i는 물품, j는 무게
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
weight[i] = Integer.parseInt(st.nextToken());
value[i] = Integer.parseInt(st.nextToken());
}
System.out.println(dfs(0, 0));
}
static int dfs(int depth, int weightSum) {
if (dp[depth][weightSum] > 0) {
return dp[depth][weightSum];
}
if (depth == N) {
return 0;
}
int valueSum1 = 0;
if (weightSum + weight[depth] <= weightLimit) {
valueSum1 = value[depth] + dfs(depth + 1, weightSum + weight[depth]);
}
int valueSum2 = dfs(depth + 1, weightSum);
dp[depth][weightSum] = Math.max(valueSum1, valueSum2);
return dp[depth][weightSum];
}
}
|
또 다음 방식으로는 bottom-up 방식의 dp를 활용해보았다. 이 방식은 링크를 보고 적용해본 방식이다.
3. dp
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
package algostudy2;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main_bj_12865_평범한배낭_dp2 {
static int N;
static int limitWeight;
static int[] weight;
static int[] value;
static int[][] dp;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
limitWeight = Integer.parseInt(st.nextToken());
weight = new int[N + 1];
value = new int[N + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
weight[i] = Integer.parseInt(st.nextToken());
value[i] = Integer.parseInt(st.nextToken());
}
dp = new int[N + 1][limitWeight + 1];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= limitWeight; j++) {
dp[i][j] = dp[i - 1][j];
if (j - weight[i] >= 0) { //i번째 물건의 무게를 취할수있다면 비교하기
//i번쨰 물건을 안취하는 경우(dp[이전물건][현재무게]) vs i번째 물건을 치하는 경우(dp[이전물건][현재무게-현재물건무게] + 현재물건가치)
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); //i번째 물건을 안취하는 경우 vs i번째 물건을 취하는 경우
}
}
}
System.out.println(dp[N][limitWeight]);
}
}
|
반응형
'Algorithm' 카테고리의 다른 글
| [BOJ] 11562. 백양로 브레이크 (0) | 2021.06.15 |
|---|---|
| [BOJ] 7579. 앱 (0) | 2021.06.12 |
| [BOJ] 1937. 욕심쟁이 판다 (0) | 2021.06.12 |
| [BOJ] 1520. 내리막 길 (0) | 2021.06.12 |
| [Programmers] 광고 삽입 (0) | 2021.06.05 |