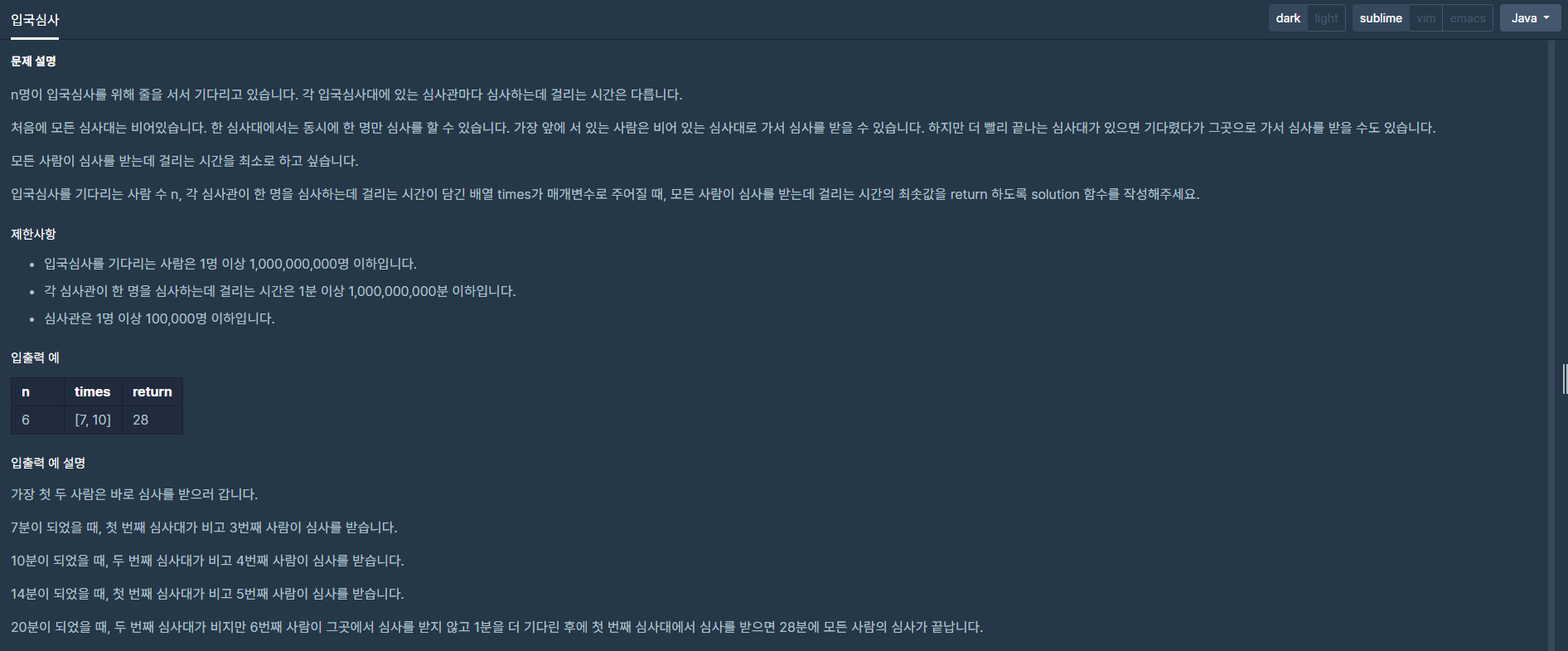
반응형
이분탐색을 사용하여 최소값을 탐색하는 문제였다.
이 문제를 접근할때 이분탐색을 접근한이유가 있다. 문제의 조건에 의해 나올수 있는 최대시간은 1,000,000,000명 * 1,000,000,000분 임으로 1중 for문으로 돌릴 수 있는 1억이 그냥 넘어가게 되어, 자연스럽게 최적을 찾을 수 있는 이분탐색을 사용해보았다. 문제에서 조심해야 할 것이 있는데 파라미터로는 int형이 들어오고 리턴형은 long형이기에 이것을 처리해주지 않으면 테스트케이스를 해결하지 못한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
package programmers;
import java.util.Arrays;
public class Solution_입국심사 {
public static void main(String[] args) {
int n=5;
int[] times = {1,1,10};
System.out.println(solution(n, times));
}
static long solution(int n,int[] times) {
long min=Long.MAX_VALUE;
long low=1;
long high=100000000000000L;
while(low<=high) {
long mid=(low+high)/2;
long temp=0;
for(long time : times) {
temp+=(mid/time);
}
if(temp>=n) {
high=mid-1;
min=Long.min(min, mid);
}else {
low=mid+1;
}
}
return min;
}
}
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
package algostudy2;
public class Solution_입국심사 {
public static void main(String[] args) {
int n = 6;
int[] times = {7, 10};
System.out.println(solution(n, times));
}
static long solution(int n, int[] times) {
long left = 0;
long right = Long.MAX_VALUE;
long answer = Long.MAX_VALUE;
while (left <= right) {
long mid = (left + right) / 2;
boolean isPossible = false;
long sum = 0;
for (int time : times) {
sum += (mid / time);
if (sum >= n) {
isPossible = true;
break;
}
}
if (isPossible) {
answer = Math.min(answer, mid);
right = mid - 1;
} else {
left = mid + 1;
}
}
return answer;
}
}
|
반응형
'Algorithm' 카테고리의 다른 글
| [Programmers] 추석 트래픽 (0) | 2020.08.07 |
|---|---|
| [Programmers] 실패율 (0) | 2020.08.03 |
| [Programmers] 스킬트리 (0) | 2020.07.30 |
| [BOJ] 4889. 안정적인 문자열 (0) | 2020.07.26 |
| [BOJ] 6198. 옥상 정원 꾸미기 (0) | 2020.07.24 |