반응형
DP를 이용하여 쉽게 구할 수 있는 문제이다.
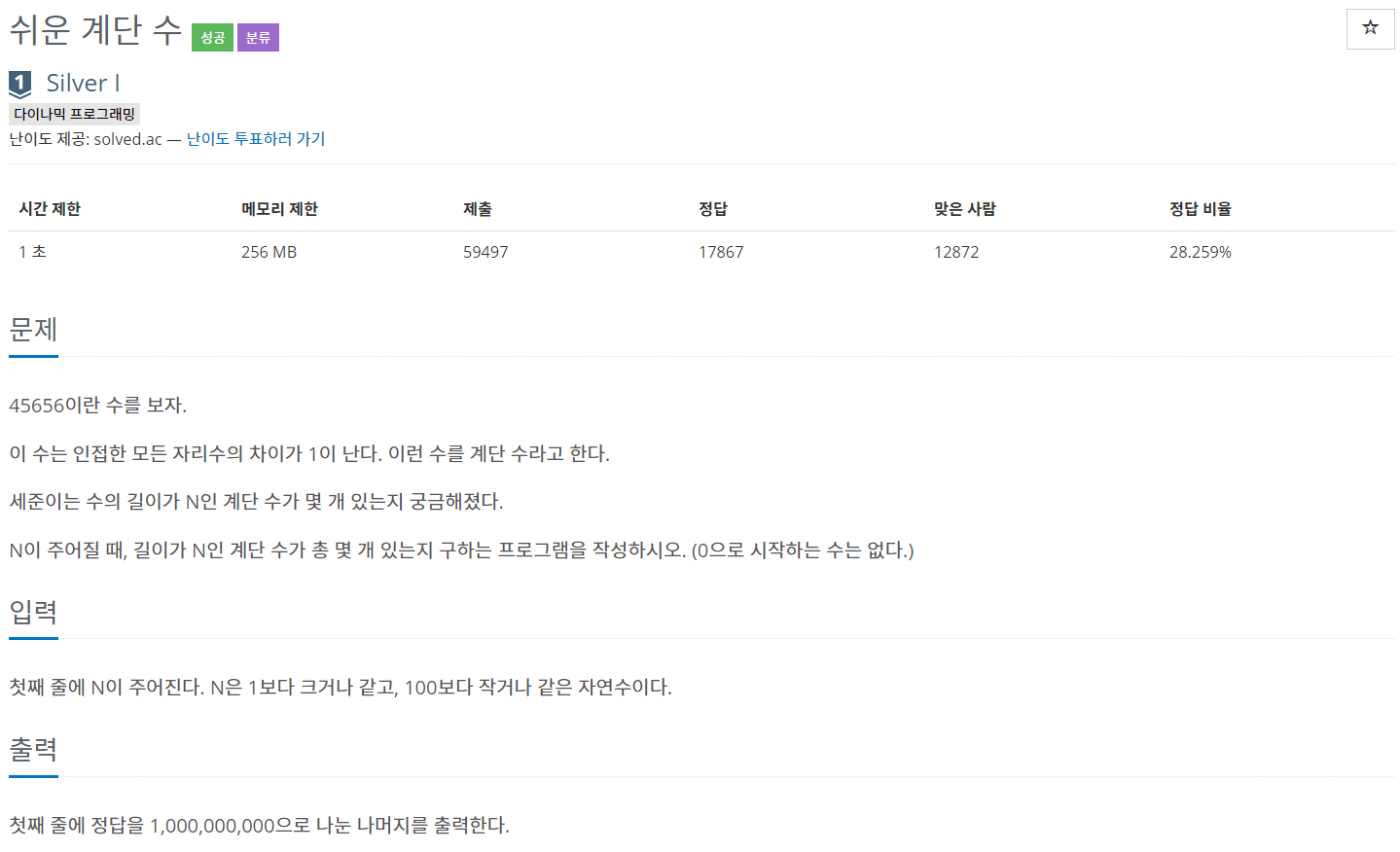
이 문제는 끝자리의 자연수가 가장 중요한 문제이다. 그래서 다음과 같은 설계를 해보았다.
dp[N][i] => N의 자리수를 가진 자연수 중에서 i의 수를 맨끝 자리로 가지는 자연수, 예를 들면 534 는 dp[3][4]에 속하는 하나의 자연수가 된다.
이와 같은 것을 이용하여 다음과 같은 점화식을 세웠다.
dp[N][i]= dp[N-1][i-1] + dp[N-1][i+1] 단, i=0일땐 i+1 만 i=9일땐 i-1만 해준다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
package boj.base;
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Main_bj_10844_쉬운계단수 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N=Integer.parseInt(br.readLine());
int[][] dp=new int[N+1][10];
for(int i=1;i<=9;i++)
dp[1][i]=1;
for(int i=2;i<=N;i++) {
dp[i][0]=dp[i-1][1] % 1000000000;
for(int j=1;j<=8;j++) {
dp[i][j]=(dp[i-1][j-1]+dp[i-1][j+1]) % 1000000000;
}
dp[i][9]=dp[i-1][8] % 1000000000;
}
long result=0;
for(int i=0;i<=9;i++) {
result+=dp[N][i];
}
System.out.println(result% 1000000000);
}
}
|
반응형
'Algorithm' 카테고리의 다른 글
| [BOJ] 4889. 안정적인 문자열 (0) | 2020.07.26 |
|---|---|
| [BOJ] 6198. 옥상 정원 꾸미기 (0) | 2020.07.24 |
| [BOJ] 1, 2, 3 더하기 5 (0) | 2020.07.05 |
| [BOJ] 11052. 카드 구매하기 (0) | 2020.07.03 |
| [BOJ] 11727. 2xn 타일링2 (0) | 2020.07.03 |